How to Add a Footer in Excel (Text, Picture, Page Numbers, and More)

Today we’ll have a look at how to add a footer in Excel and we’ll be talking about how to insert a text, a picture or page numbers into the footer of an Excel document in a quick and easy way.

Shall we start?

Would you rather watch this tutorial? Click the play button below!

How to Display Footer in the Sheet

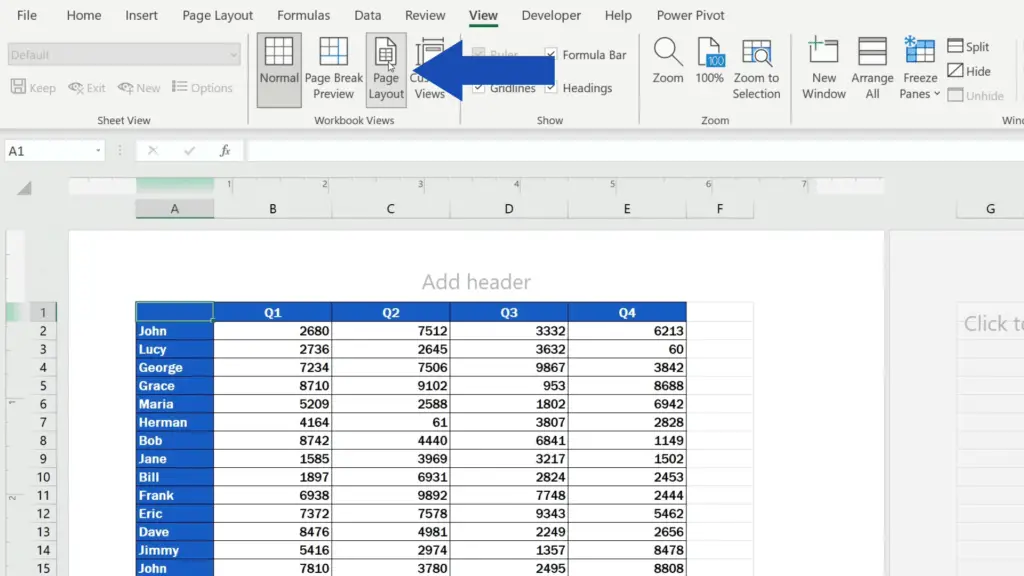
First of all, we need to display the footer in the sheet, so we’ll go to the View tab and click on ‘Page Layout’.

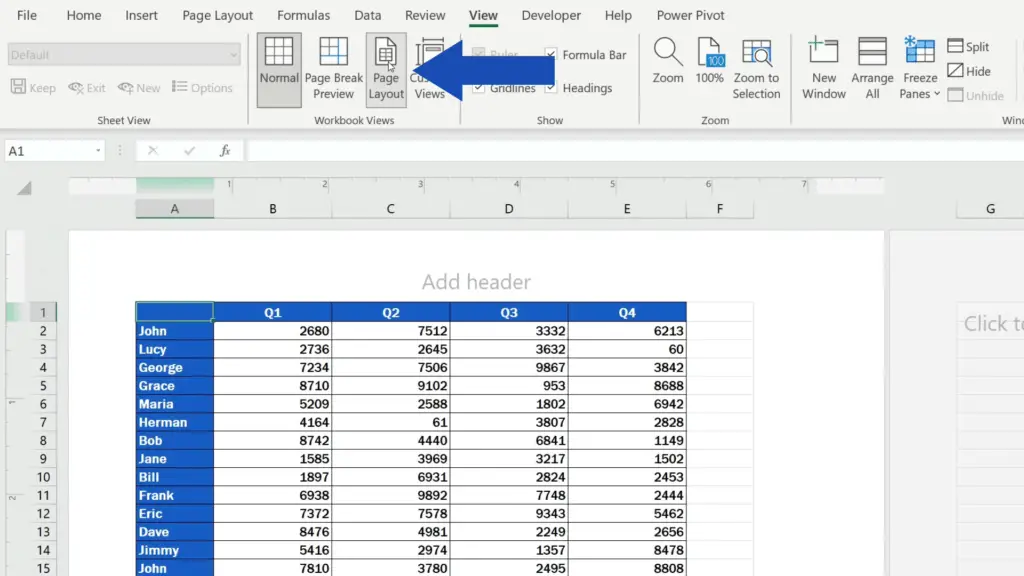
Then we click anywhere at the bottom of the document to see these three sections. This is the place where we can insert various elements in the footer.

How to Add Page Numbers to the Footer

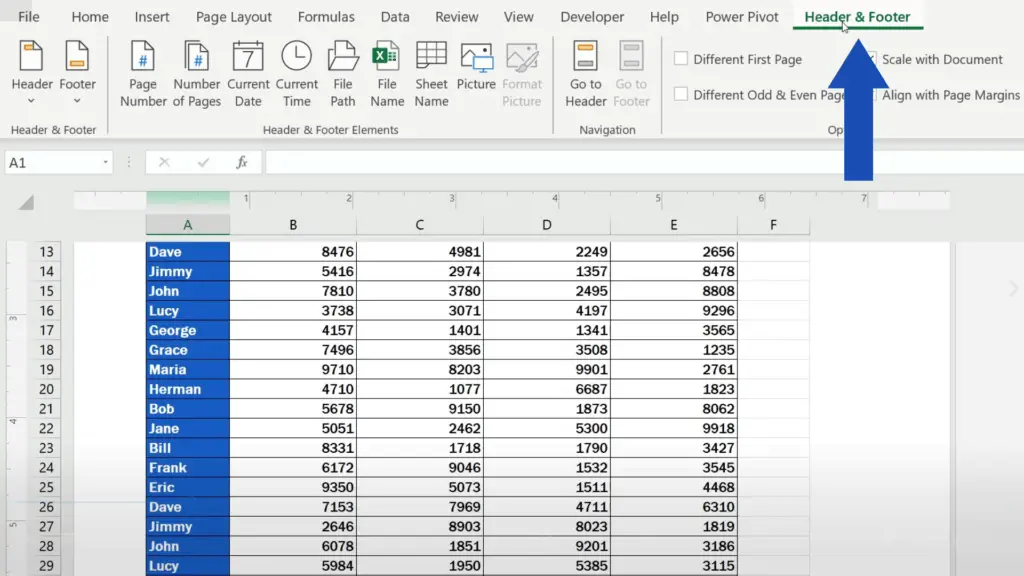
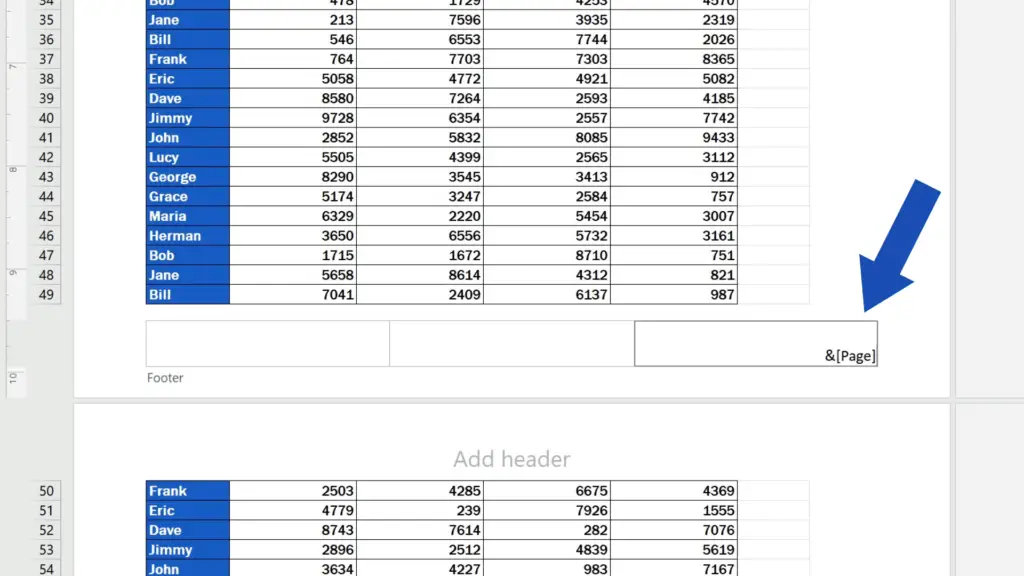
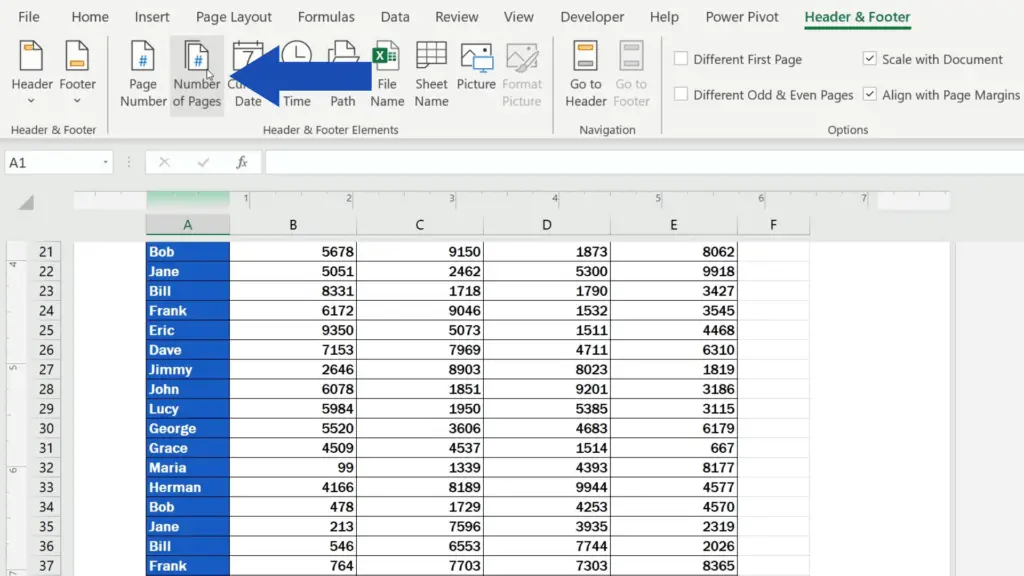
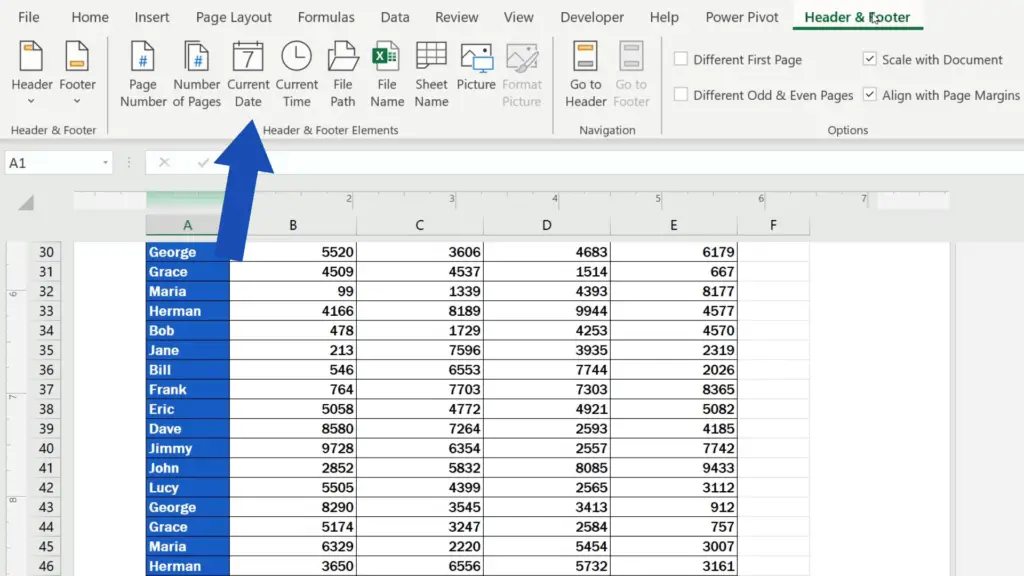
Let’s say we would like to insert page numbers in the right part of the footer. Click into the selected footer section, then go to the Header & Footer tab on the Ribbon and select ‘Page Number’.

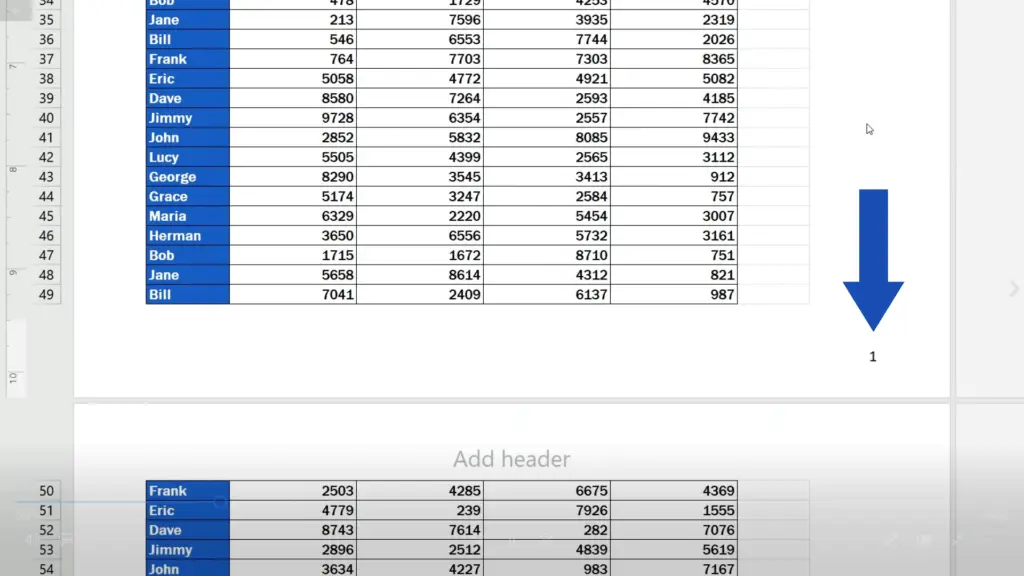
Excel uses this code for page numbers, so if we now click anywhere within the document area, the footer shows the number of the page there.

To add a total page count to the page numbers, simply click into the footer again, type in a forward slash to separate the two numbers and then click on ‘Number of Pages’.

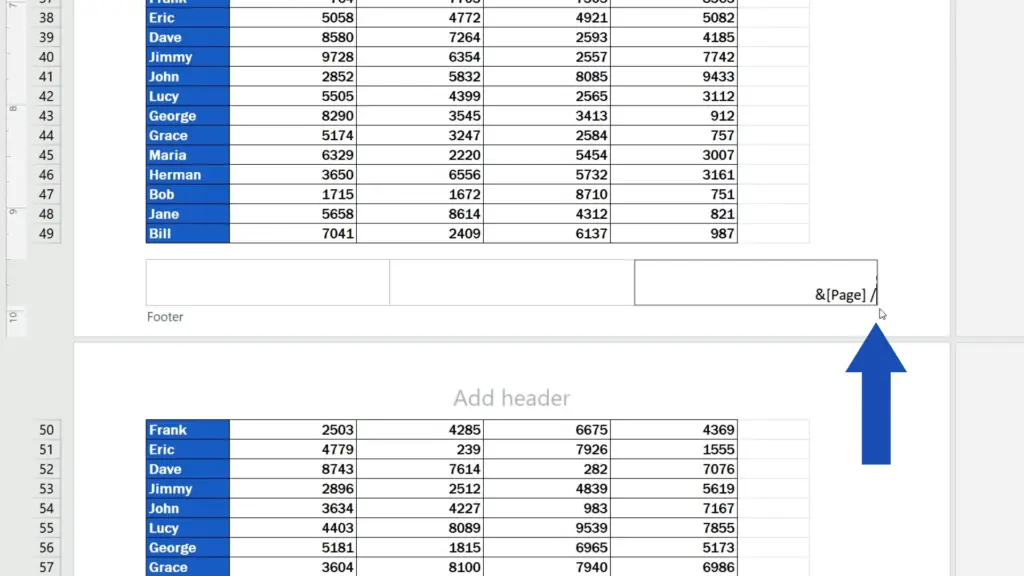
Again, we can see a code here, but once we click outside the footer area, what shows after the page number is the number of pages separated with a slash – just as we wanted.

We can use the same way to insert, for example, ‘Current Date’, ‘File Path’, ‘File Name’ or the ‘Sheet Name’.

Let’s carry on and have a look at how to insert a picture, because there are a couple things that are worth mentioning about that.

How to Add Picture to the Footer

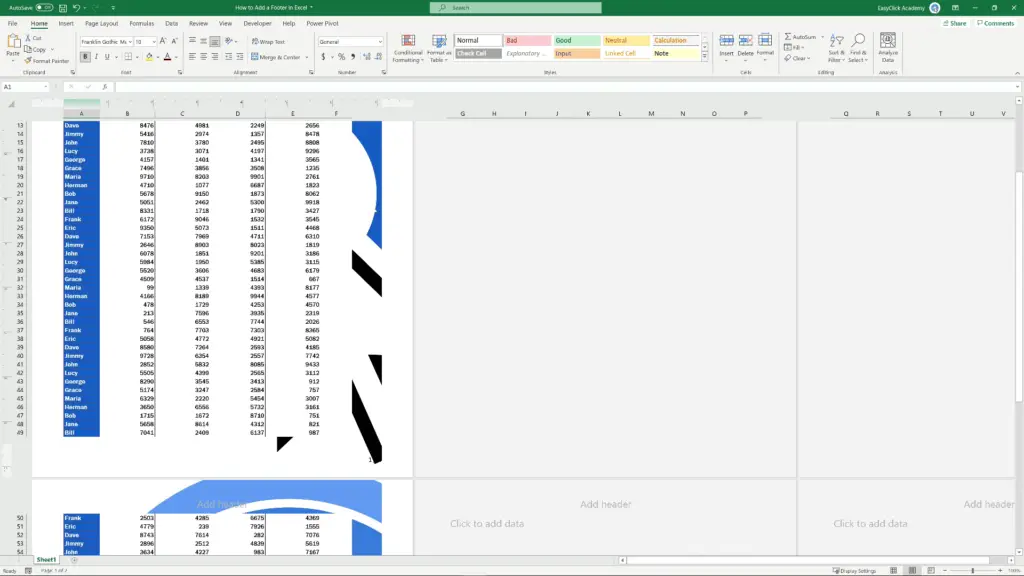
Imagine we want to add a logo into the footer section on the left. Let’s click there, go to ‘Header & Footer’ and there we click on ‘Picture’.

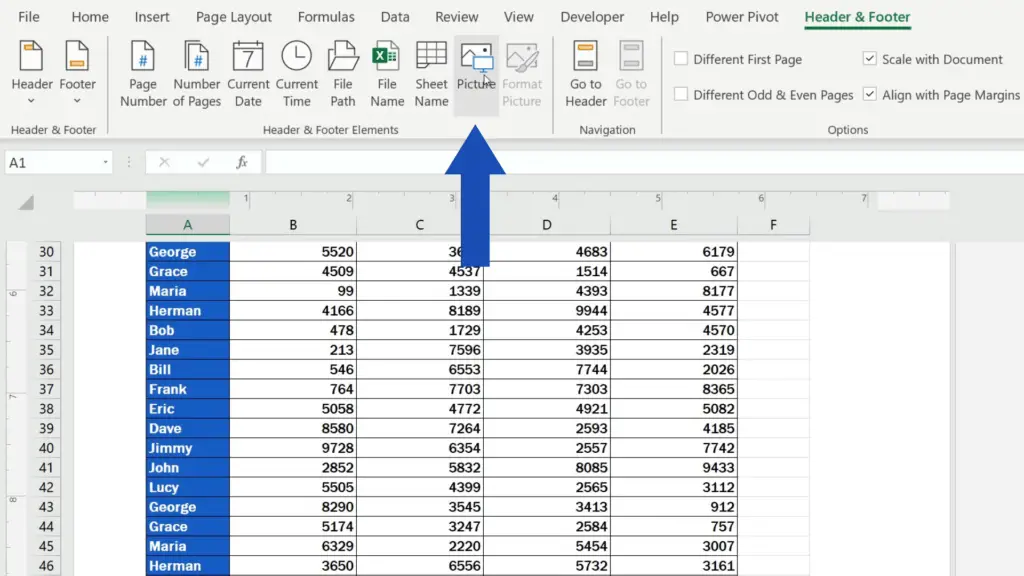
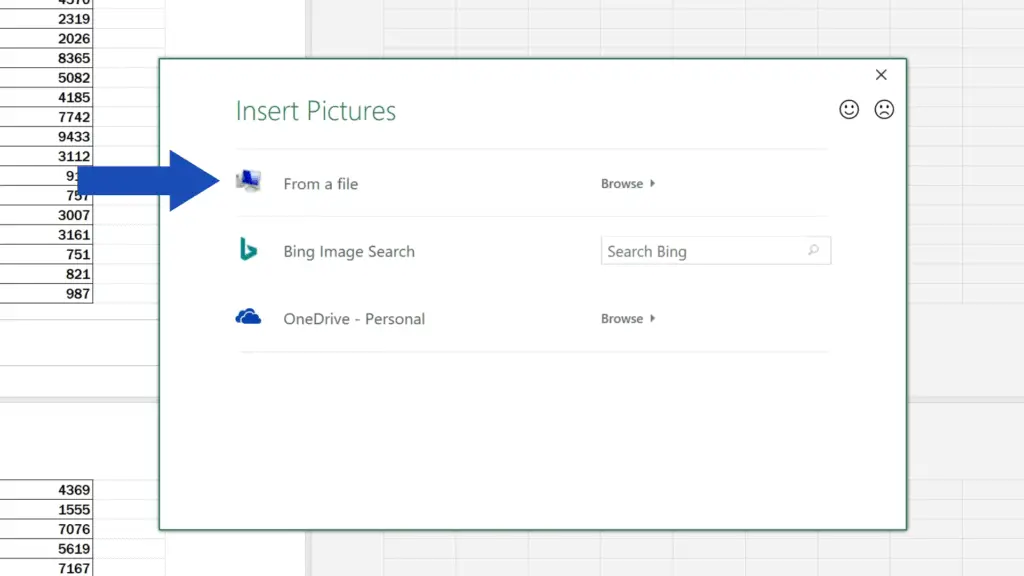
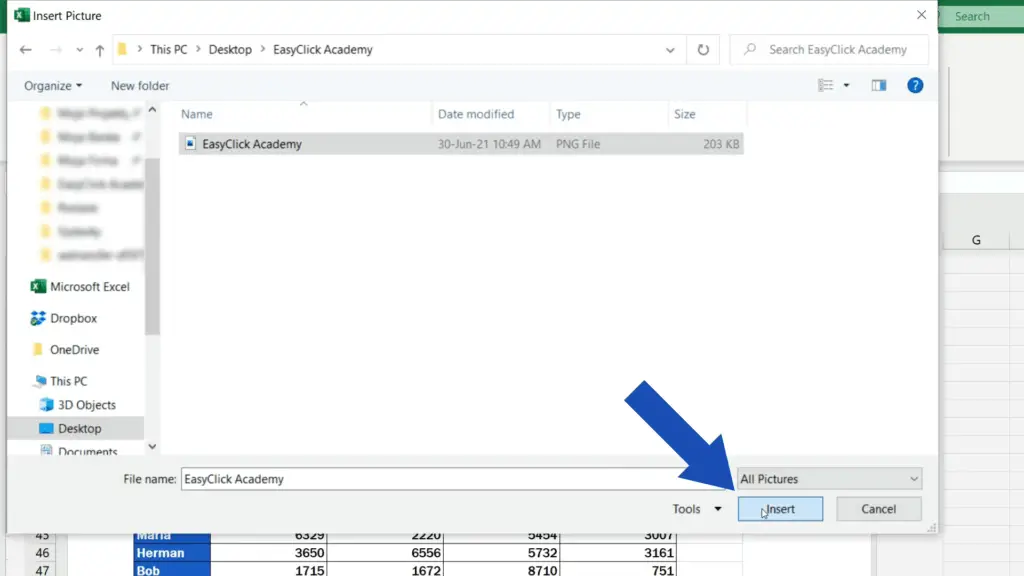
Excel will show several options of locations which we can browse to add the picture. Here we’ve got the logo ready on our computer drive, so we’ll select the first option and find the folder where the picture’s been prepared. We’ll click on it and confirm with the ‘Insert’ button.

Again, we can see a code in the footer and again, we click anywhere into the document area to see the picture we’ve just inserted, which is obviously way too big.

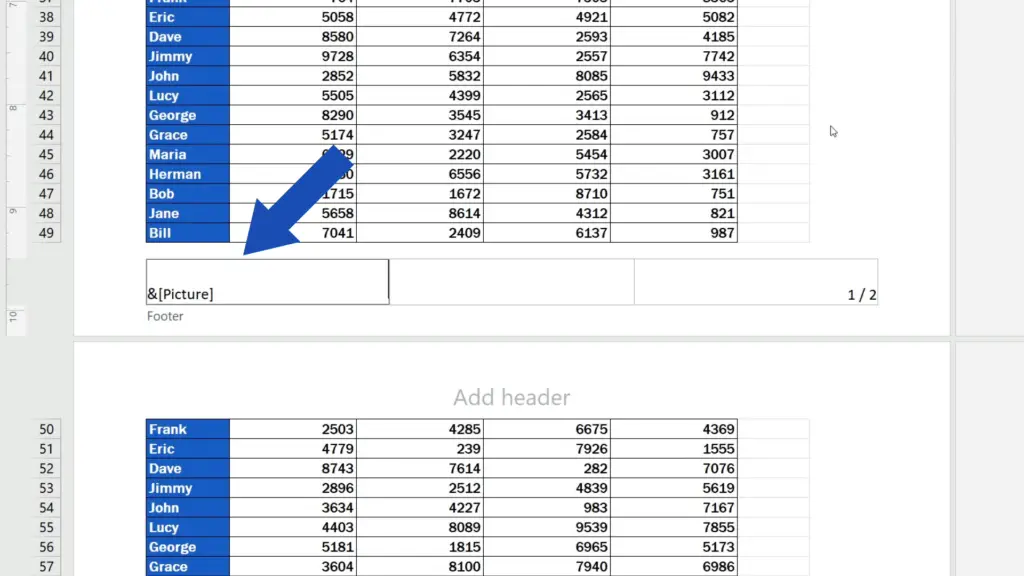
But that’s no problem at all because we can format it just as we need.

Click on the left section of the footer again, go to the tab ‘Header & Footer’ and choose the option ‘Format Picture’.

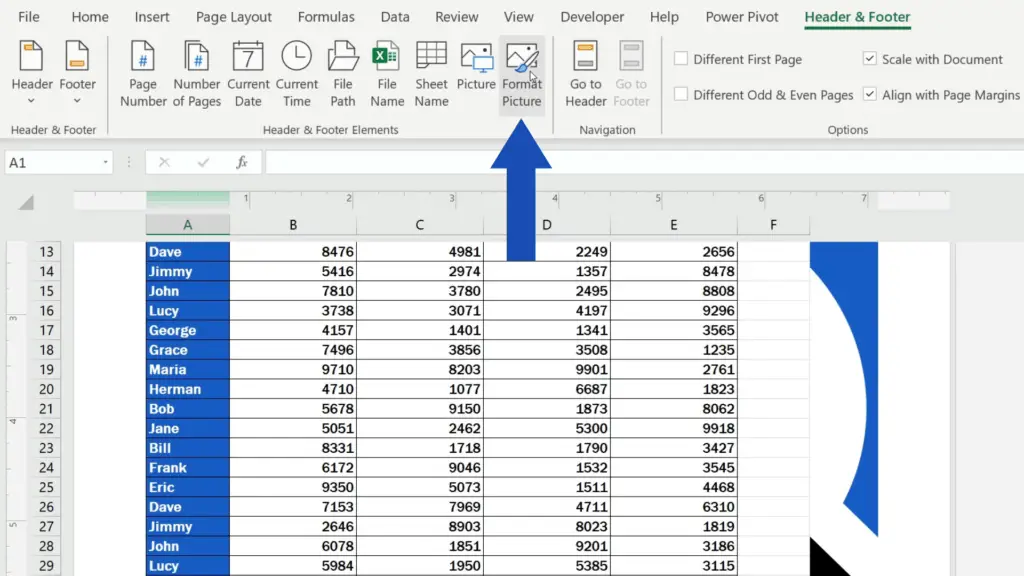
You’ll see this window where you can find all you need to make changes to the inserted picture.

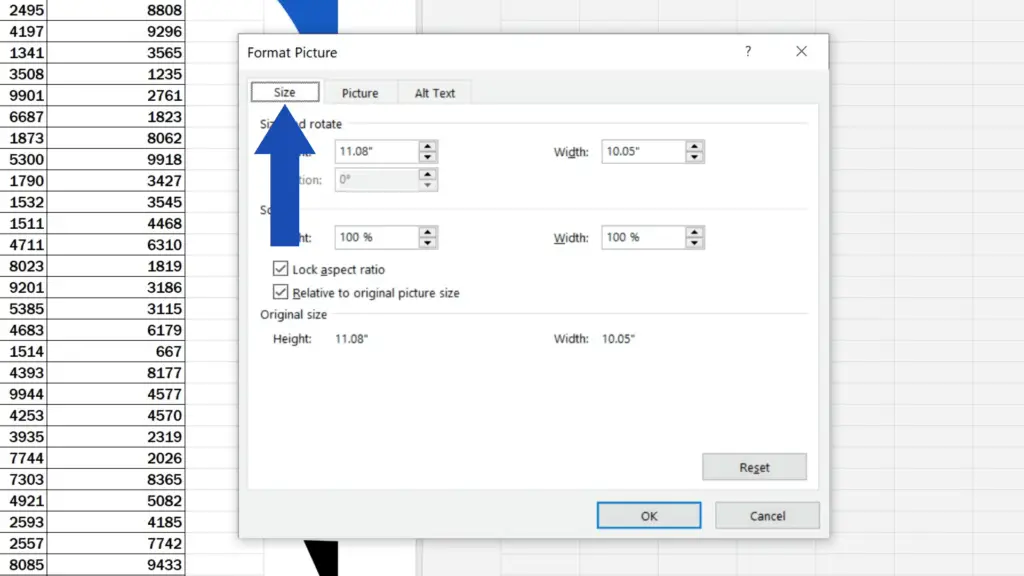
In this case, we’ll focus on its size. We can change it through specifying the exact numbers for its height and width or by changing the percentage under the section ‘Scale’. Now we’ll use the Scale option and we’ll set the height to 7%.

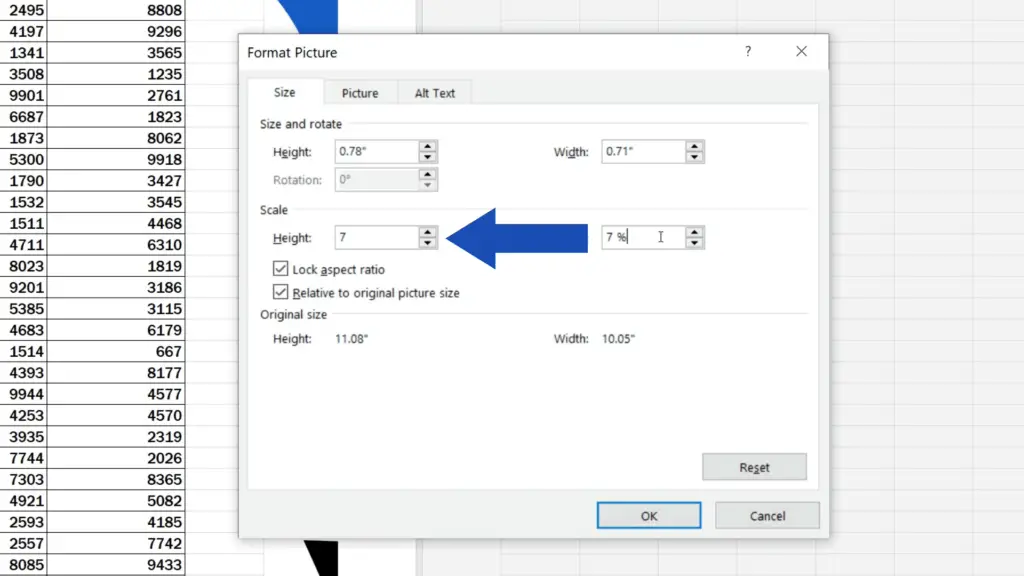
When we click on OK, the picture will appear resized as needed.

If any of the inserted elements overlaps the document area, like in the case of the logo here, the border of the footer can be easily moved here, on the left.

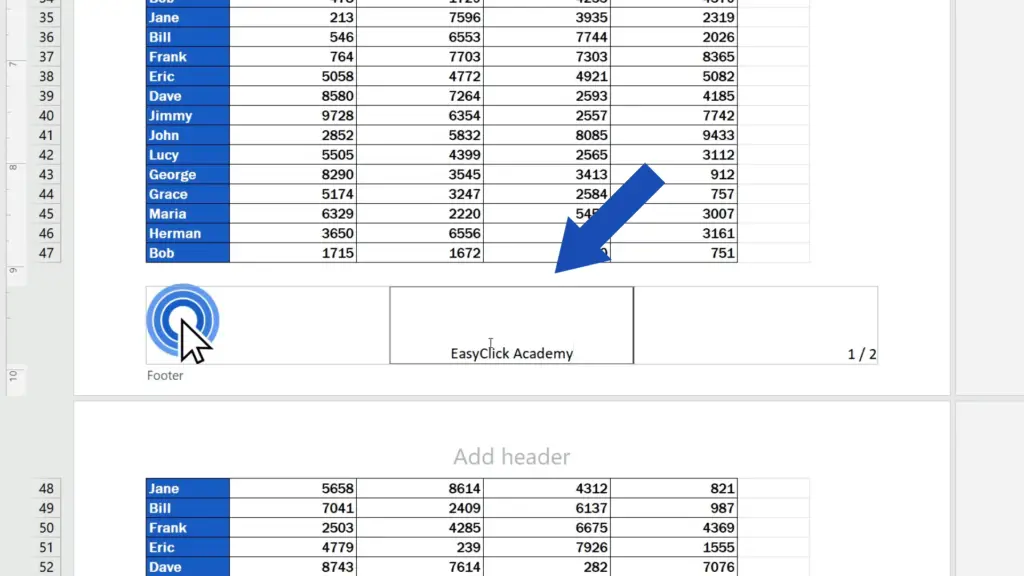
And here we go – let’s give it a try with text, too, which is nothing difficult.

How to Add Text to the Footer

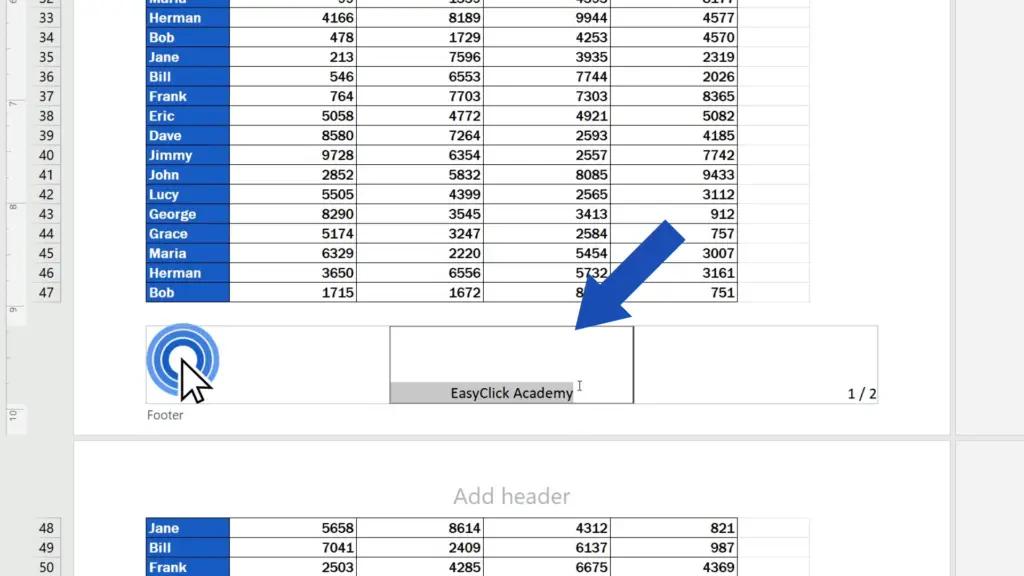
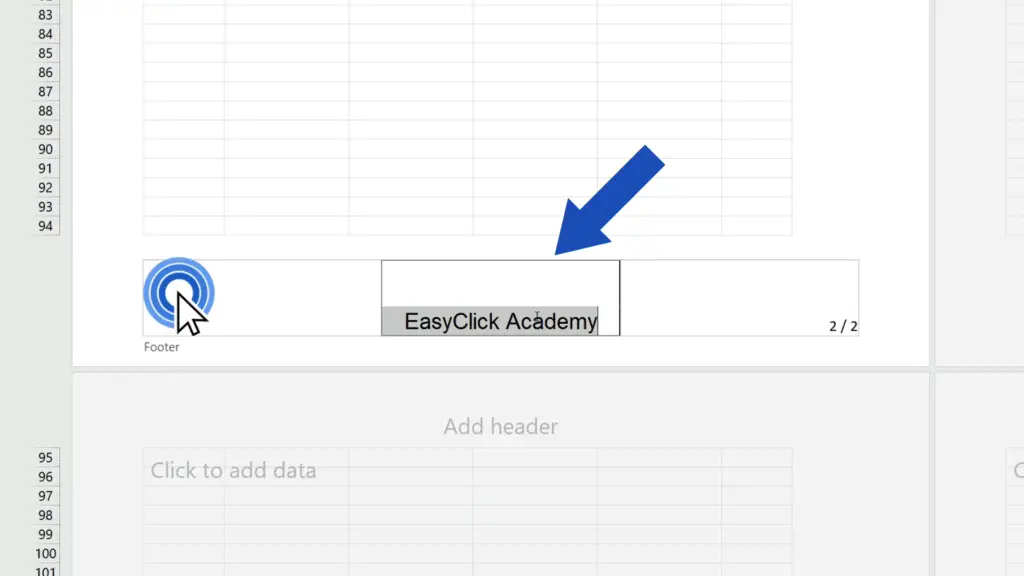
Click on the footer part where you need to insert the text – here we’ll type in ‘EasyClick Academy’ and that’s it!

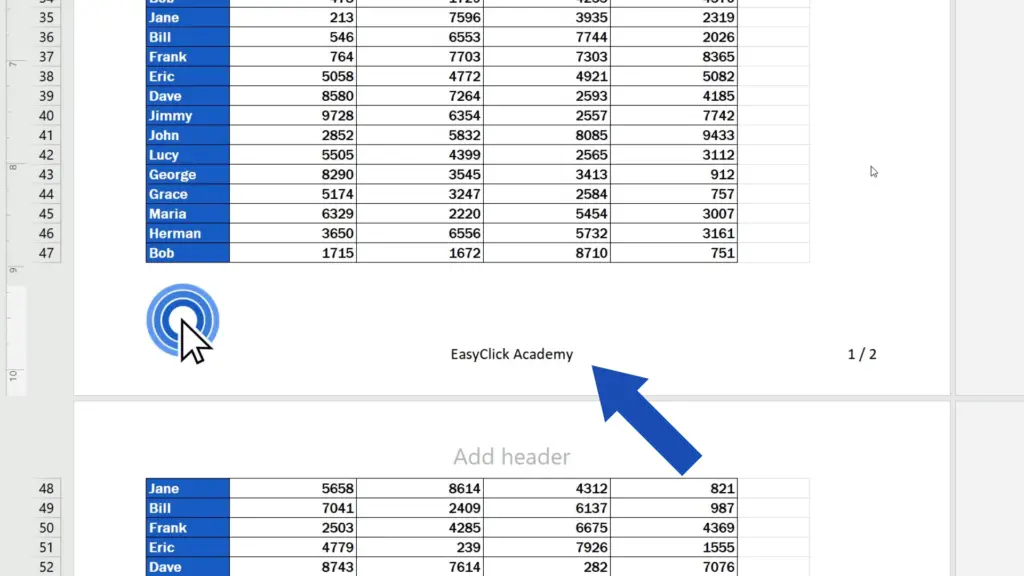
Now click anywhere in the spreadsheet and the text will show in the footer of the document.

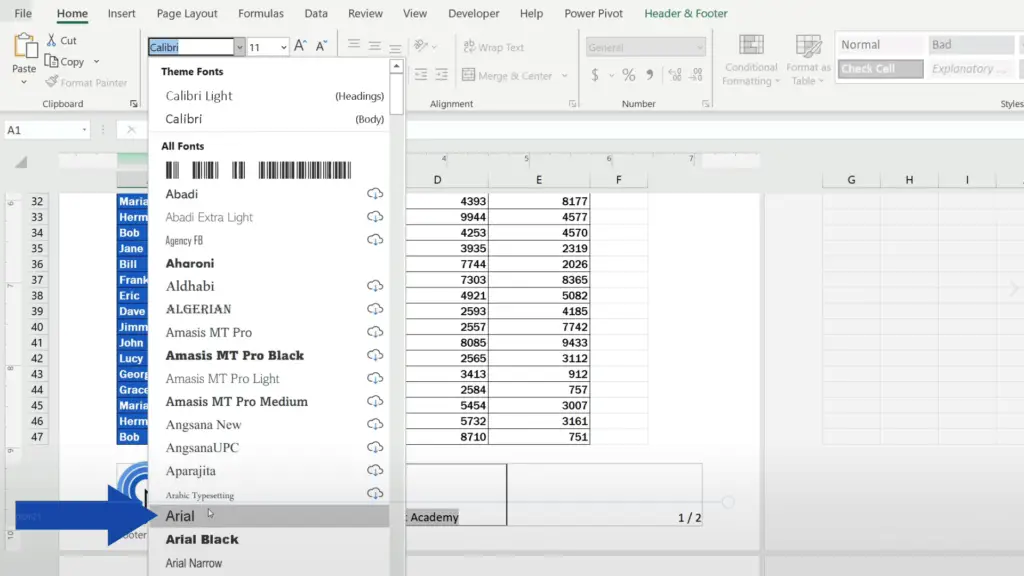
Of course, you can adjust the font type, size and colour of the text in line with the document style. Here we’ll change the font type and its size.

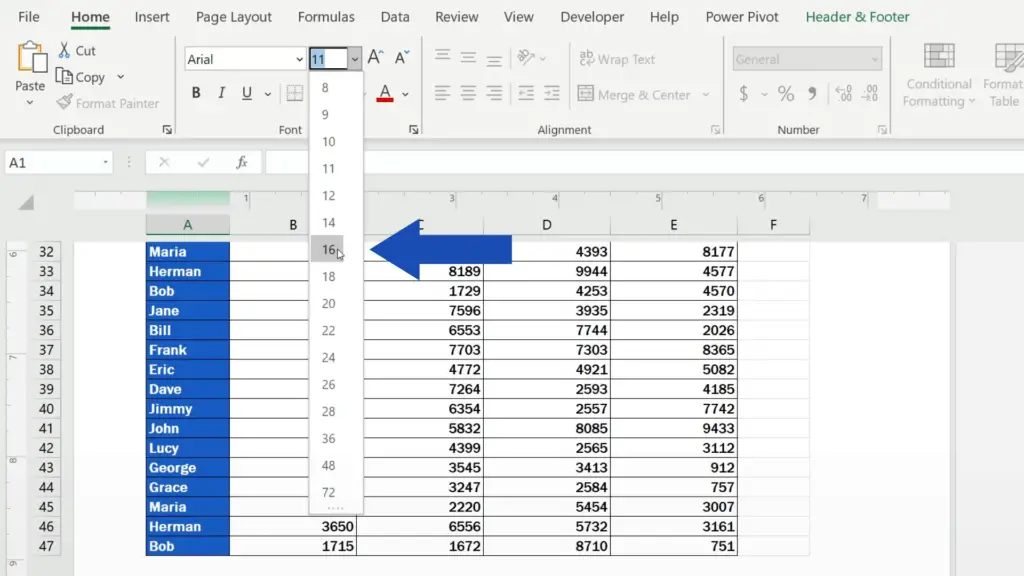
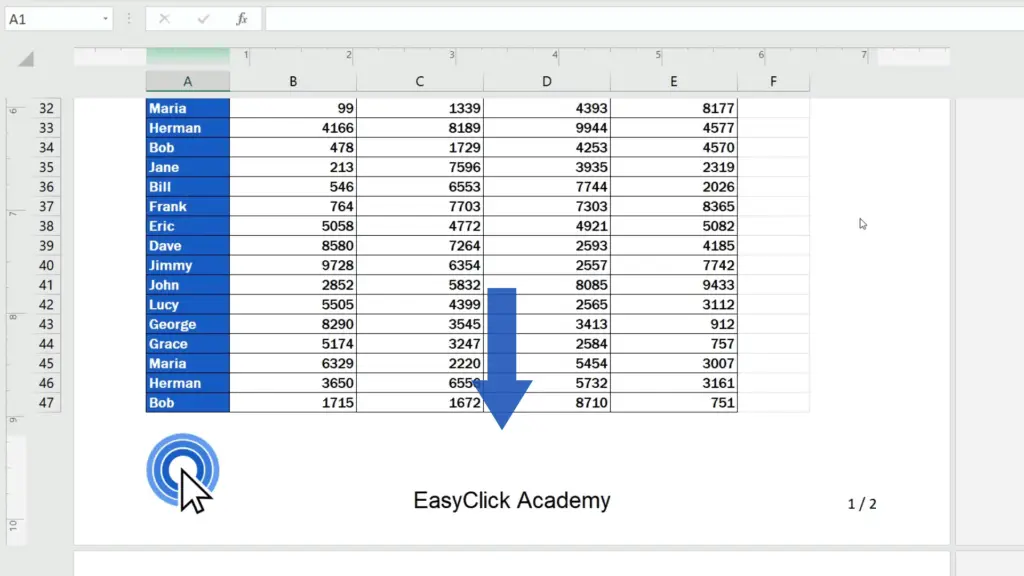
We’ll highlight the text, go to the Home tab and we’ll change the font to Arial and set the size to 16. Great!

And let’s have a look at a few more interesting tips.

How to Add Different Footer on the First Page

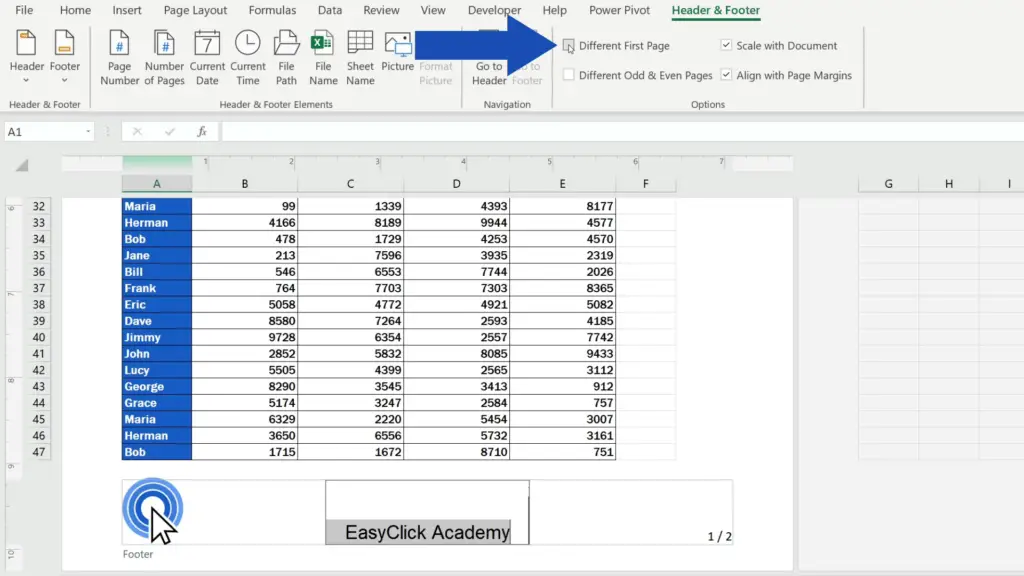
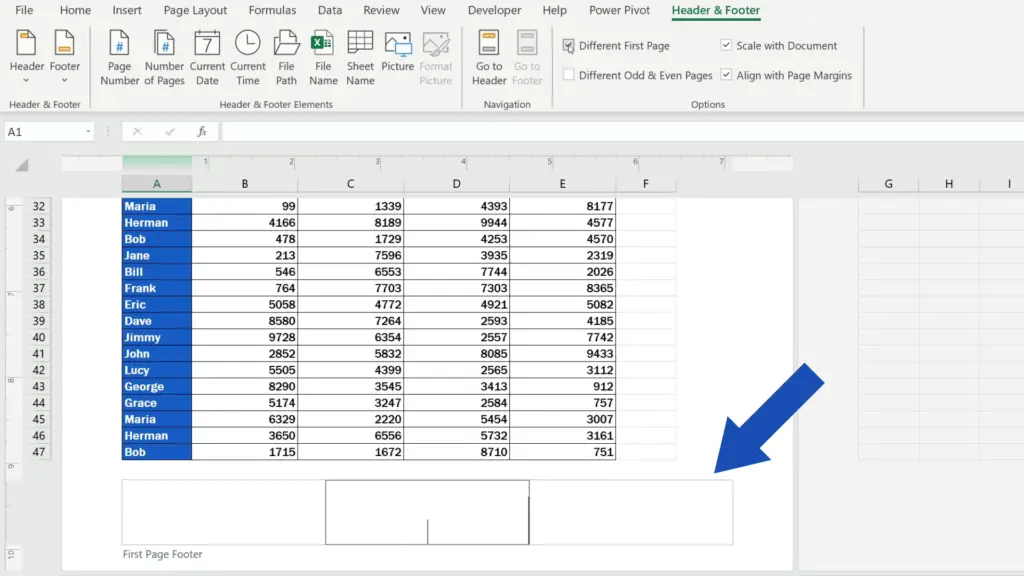
If you need to have a different footer on the first page of the document, it can be done in a quick and easy way.

Click into the footer, open ‘Header & Footer’ and select ‘Different First Page’, which allows you to modify the footer on the first page and, at the same time, this will not affect the footers on the rest of the pages.

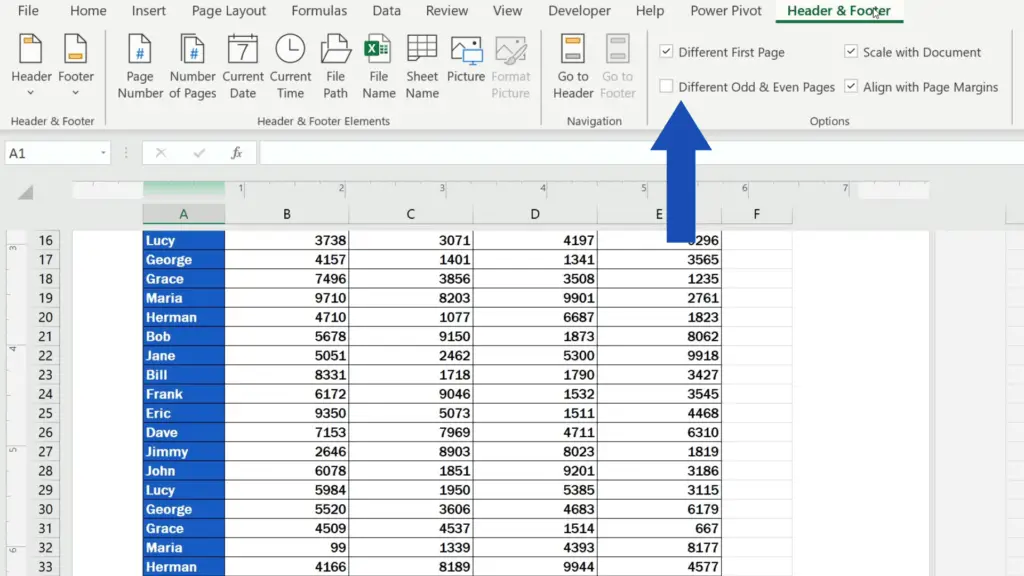
In addition, this section contains other useful options, for example, you can set ‘Different Odd & Even Pages’, through which you can basically make the footers on the odd pages different from the footers on the even pages.

And of course, you can remove any element from the footer anytime.

How to Remove Any Element From the Footer

Simply click on it and delete it. For example, the text ‘EasyClick Academy’ – we’ll select it, press Delete and that’s all it takes!

All these little tricks work well with the header of the document, too. To see the tutorial that deals with the header, check out the link in the list below!

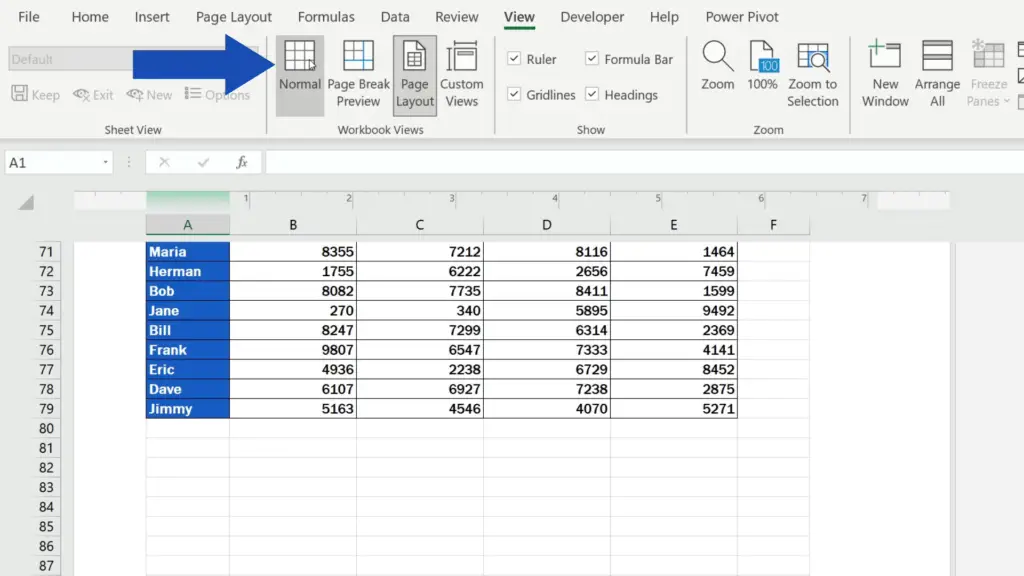
After you’re done with the footer, you can return to the regular view through the View tab, selecting the view ‘Normal’.

Don’t miss out a great opportunity to learn:

• How to Add a Header in Excel (Text, Picture, Page Numbers, and More)
• How to Insert a Watermark in Excel (Picture or Text)
• How to Convert an Excel File into PDF

If you found this tutorial helpful, give us a like and watch other tutorials by EasyClick Academy. Learn how to use Excel in a quick and easy way!

Is this your first time on EasyClick? We’ll be more than happy to welcome you in our online community. Hit that Subscribe button and join the EasyClickers!

Thanks for watching and I’ll see you in the next tutorial!